①ルートの中身を簡単にする 分数を書くときは \(\dfrac{6}{4}=\dfrac{3}{2}\) のように可能な限り「約分」をしますよね。 それと同じで、平方根を使って数を表すときは ルートの中身を可能な限り小さな自然数 にします。
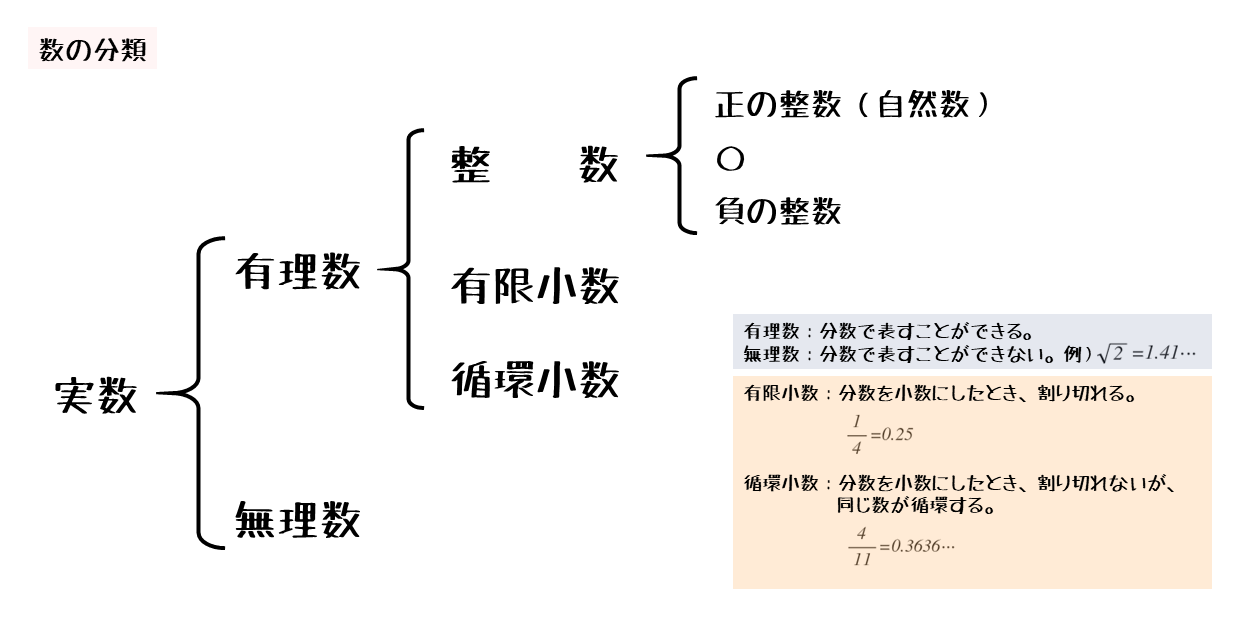
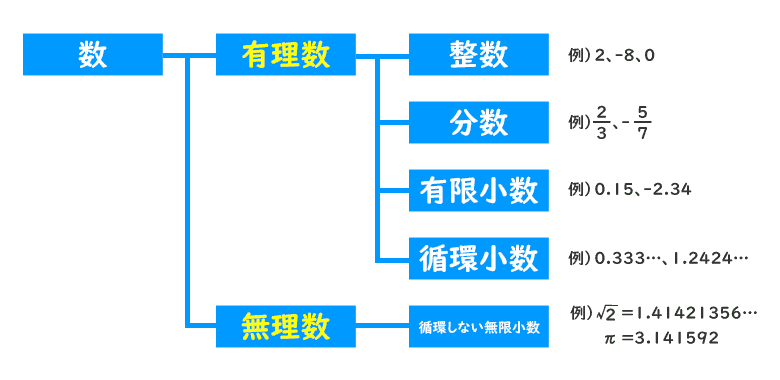
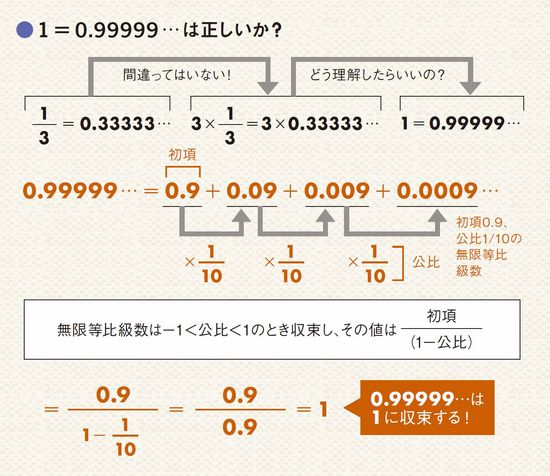
分数 ルート 少数部分- ルート2は、なぜ無限(・・・)に続くのか?の証明 前提その1 1/2 = 05など、分数で表せる値は、無限小数ではない(有理数=分数で表せる数) 前提その2 1/3 = ・・・など有理数だが、無限小数もある(ただし必ず循環小数=同じ値の繰り返し) 平方根(ルート)の掛け算がわかる5ステップ 平方根の掛け算は5ステップで計算できるよ。 ルートを簡単にする 整数同士をかける 平方根同士をかける くっつける ふたたびルートを簡単にする えっ。 5ステップもあるからダルいって!
分数 ルート 少数部分のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | 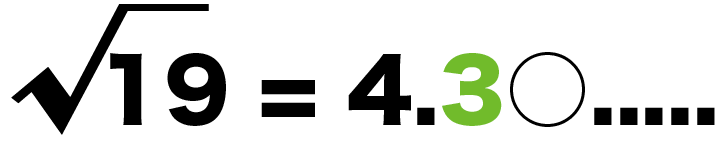 |
 |  |  |
 | 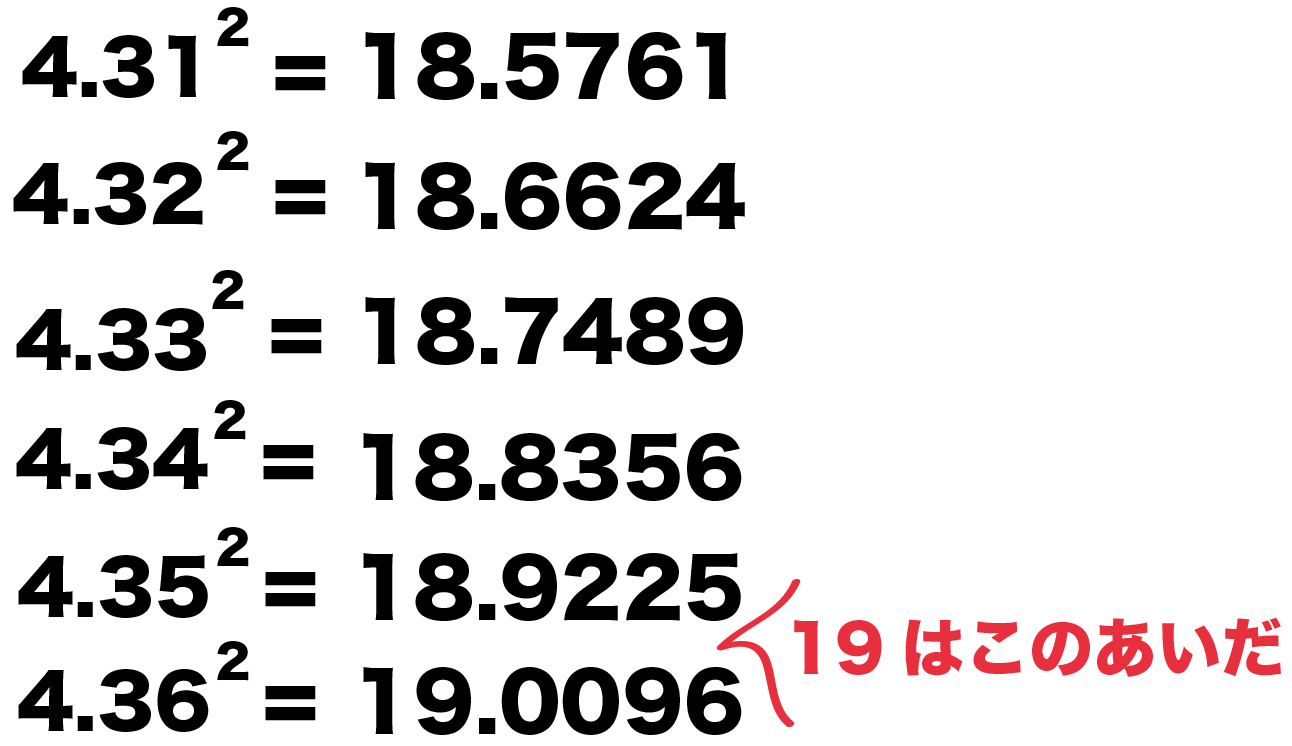 |  |
 |  | |
「分数 ルート 少数部分」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
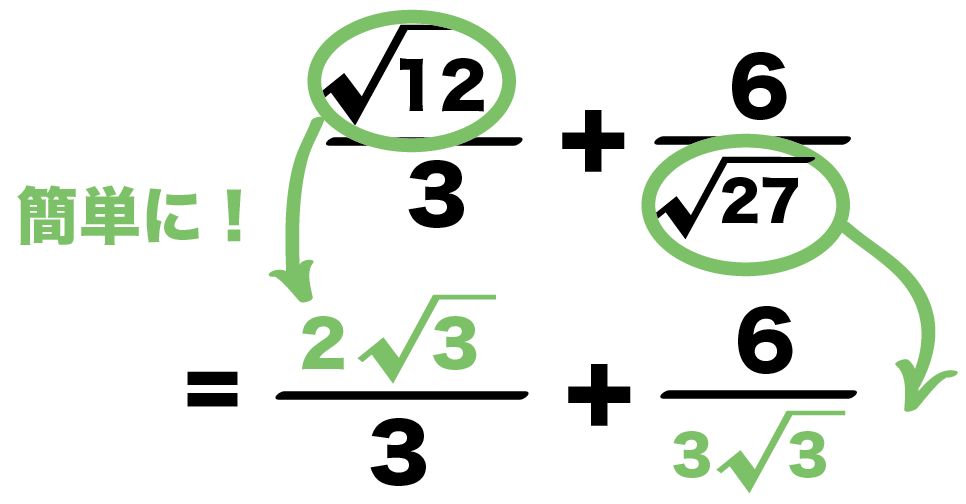 |  |  |
 |  |  |
「分数 ルート 少数部分」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「分数 ルート 少数部分」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 |  | |
「分数 ルート 少数部分」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 |  |  |
「分数 ルート 少数部分」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
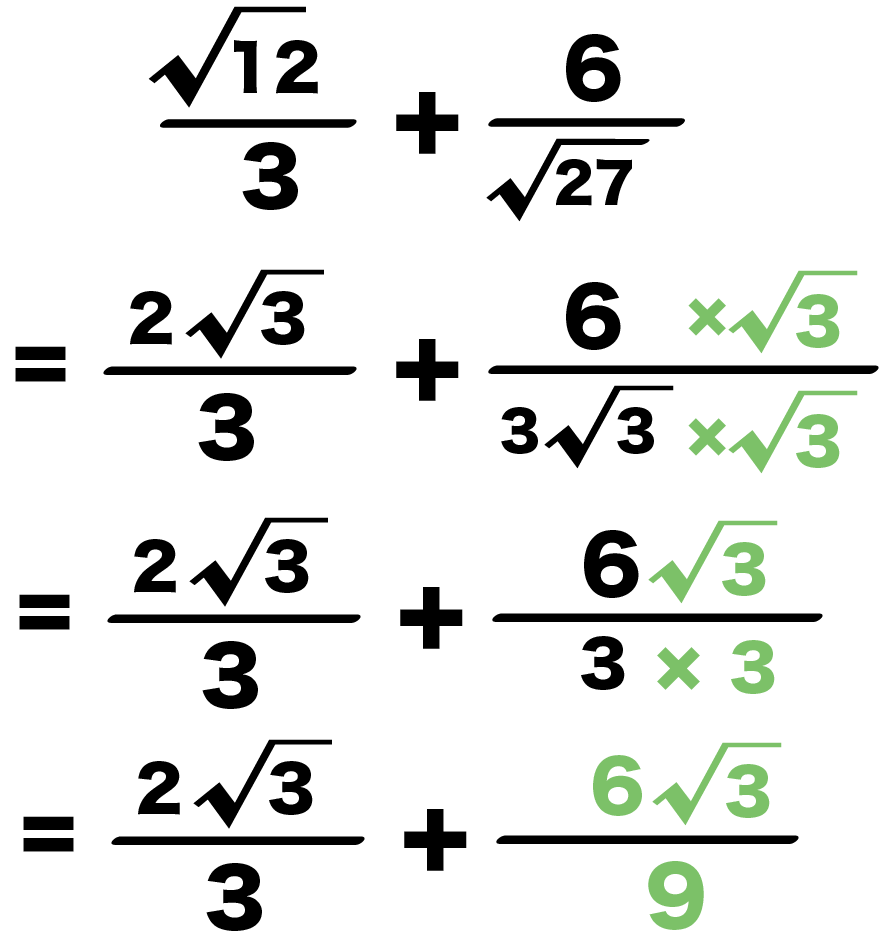 |  |  |
「分数 ルート 少数部分」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
 |  |  |
「分数 ルート 少数部分」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 |  |  |
「分数 ルート 少数部分」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |
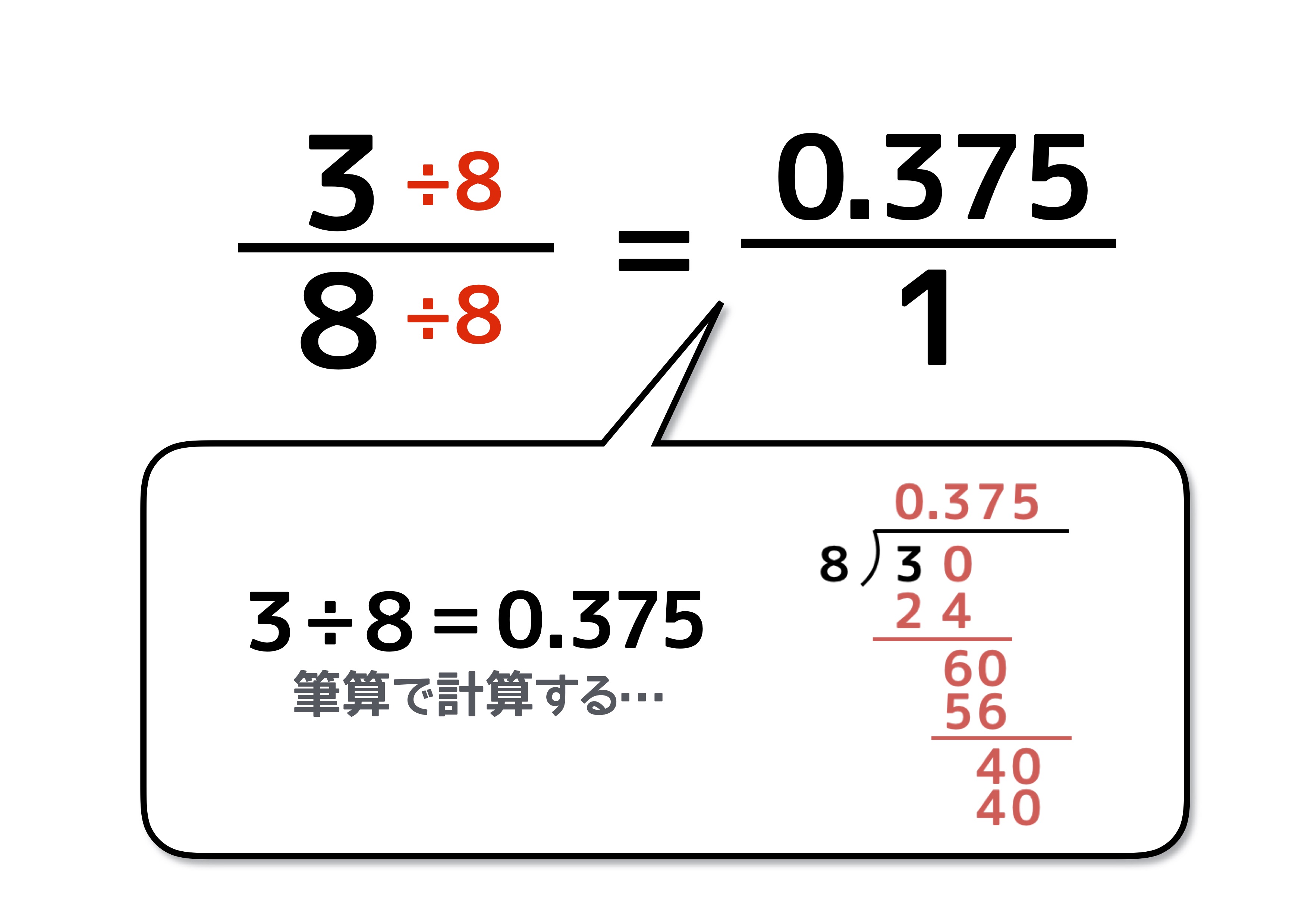
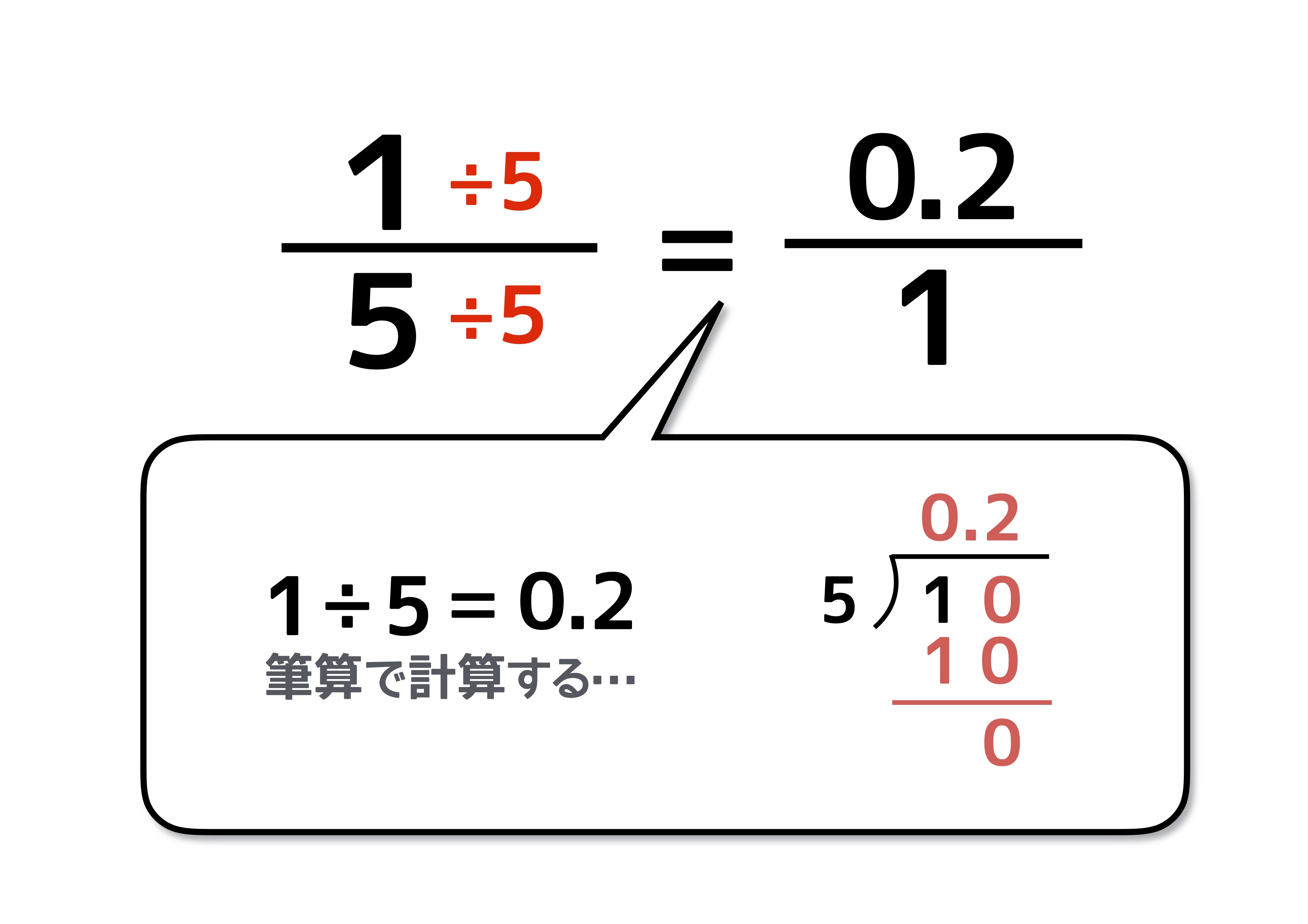
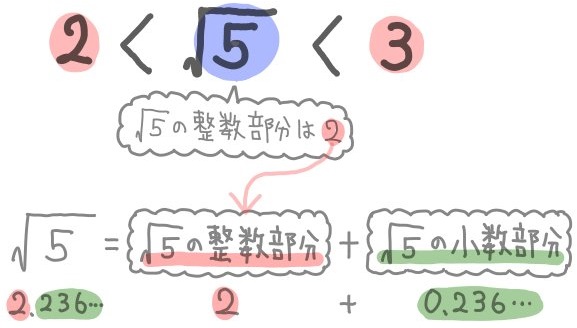
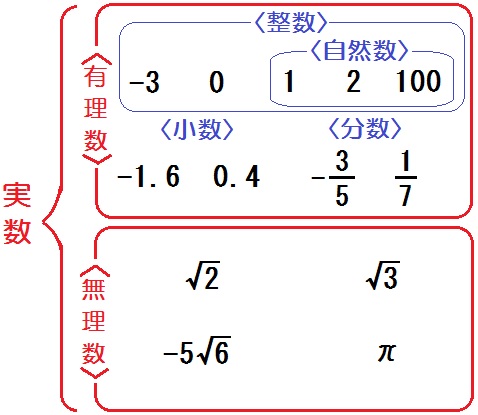
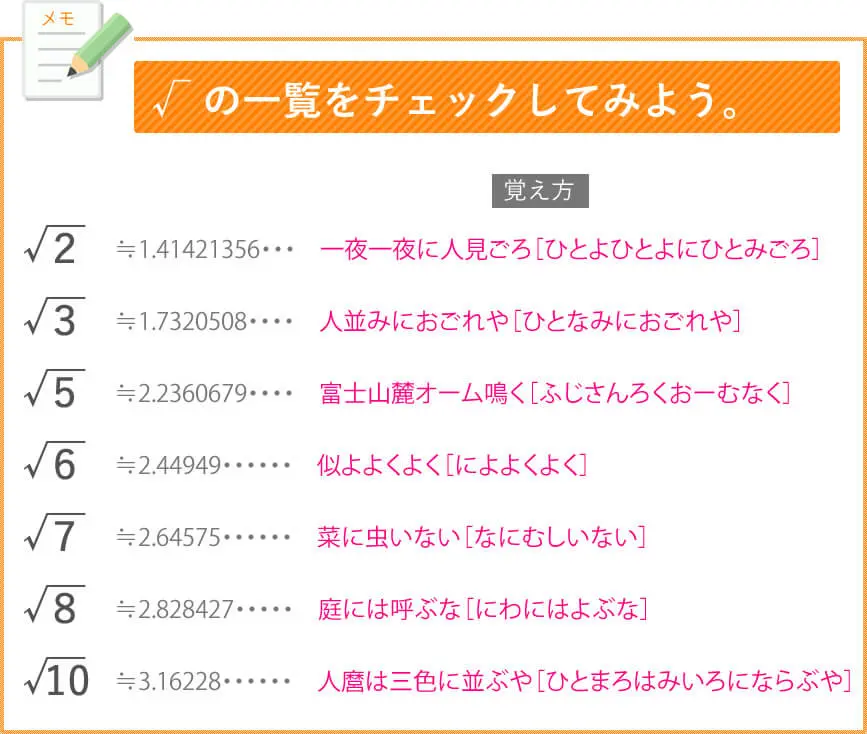
ただし,ルート2,ルート3,ルート5の近似値とその語呂合わせは非常に有名なので教養として覚えておくとよいでしょう。 平方数でない正の整数 n n n に対して n \sqrt{n} n は無理数(→ルート2が無理数であることの4通りの証明)なので小数は無限に続きます。小数を分数に変換する方法 変換段階 小数の小数は、小数のピリオドの右側の桁の分数(分子)と10の累乗(分母)として記述します。 分子と分母の最大公約数(gcd)を見つけます。 分子と分母をgcdで割って、分数を減らします。 例1 032を分数に変換し
Incoming Term: ルート 分数 少数, 分数 ルート 少数部分,




0 件のコメント:
コメントを投稿